++ 50 ++ 3平方の定理 角度 150125-3平方の定理 角度 1辺

三平方の定理を慶應生が超わかりやすく解説 公式 証明 計算問題付き 高校生向け受験応援メディア 受験のミカタ
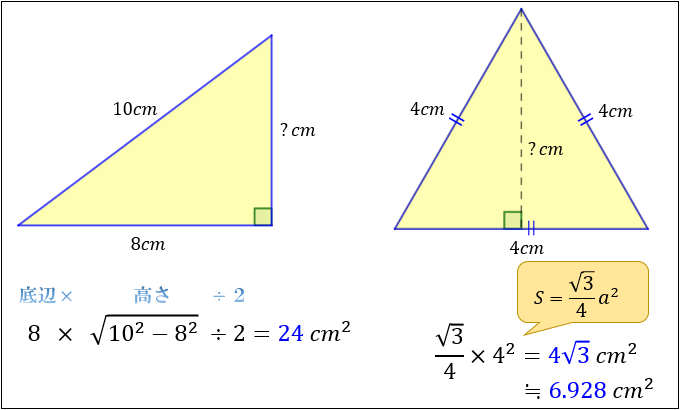
2 大人向け ピタゴラゴラスの定理の証明 21 面積図を使った証明; まとめ:三平方の定理(ピタゴラスの定理)の公式は便利だから絶対暗記! 三平方の定理(ピタゴラスの定理)の公式はめちゃくちゃ便利。 この公式なら、 長方形の対角線の長さ;
3平方の定理 角度 1辺
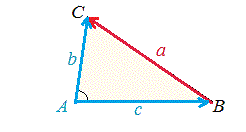
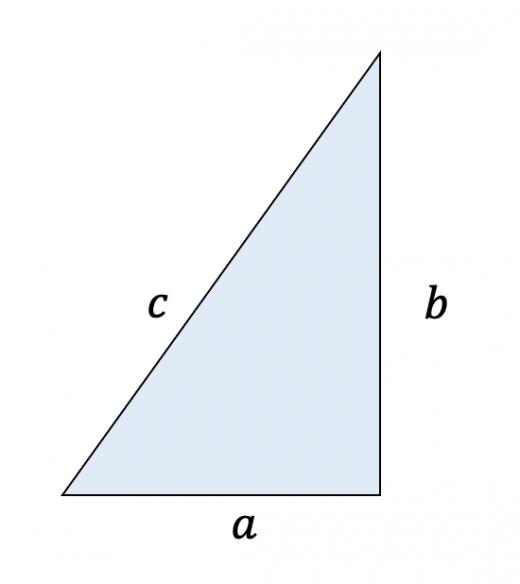
3平方の定理 角度 1辺-三平方の定理は、 直角三角形の三辺をa,b,cとする。 斜辺 (最も長い辺)をcとすると、 c² = a² b² が成り立つ というものです。 別名ピタゴラスの定理とも呼ばれます。 式は綺麗ですが、二乗が出てきます。 なので、実際にこの定理で辺の長さを計算すると、平方根を求める作業が必要になり、大変かもしれません。税理士 事務 所 個人 事業 主;
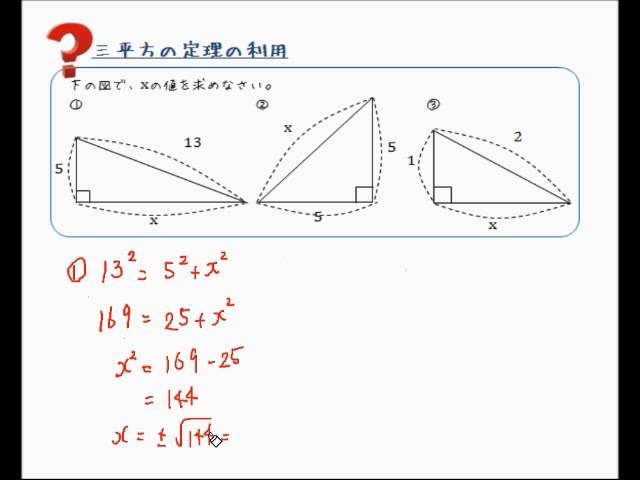
三平方の定理で辺を求める Youtube
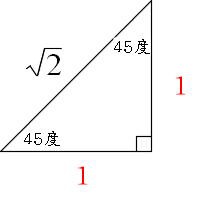
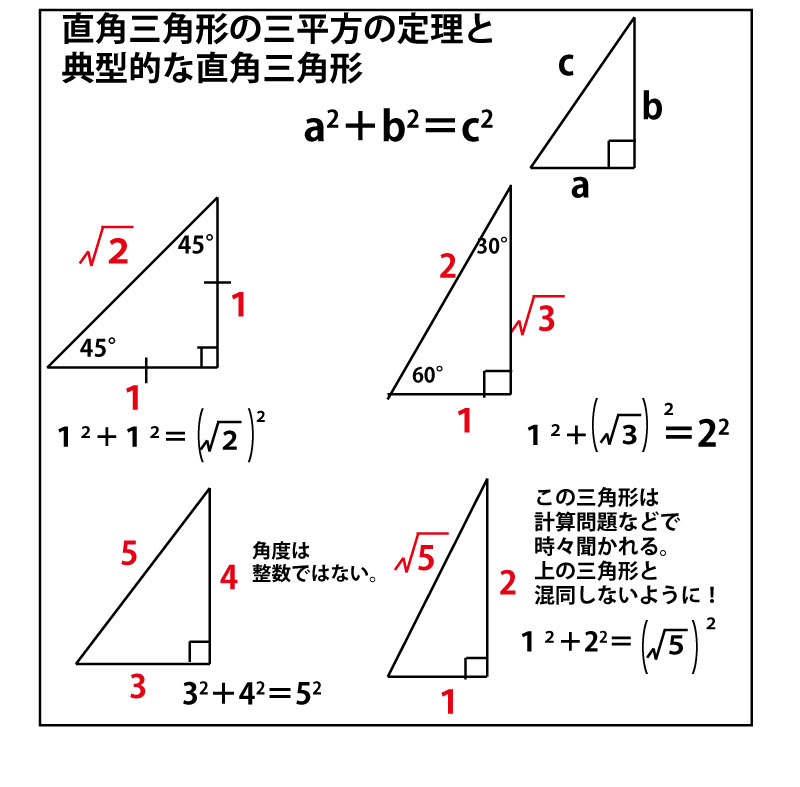
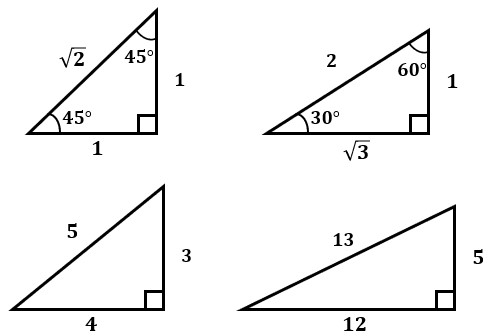
三平方の定理を満たす3つの数字には、3 つと 続いて紹介するのは、角度や3辺の比が特徴的な直角三角形。 3辺の比に平方根(ルート)が含まれますが、暗記しておけば簡単に計算できます。 慣れれば暗算で求められるようになるので、スムーズに問題が解けますよ! ⑤辺の比1:1:√2 内 ピタゴラスの定理(3平方の定理)とは ピタゴラスの定理っていうのは、 直角三角形の3辺の長さの関係を表したものだよ その関係っていうのは、$斜辺^2=底辺^2高さ^2$だよ はかせちゃん この定理には数百通りもの証明があるらしいんだけど、↓の証明が恐ろしい wikipediaより引用 345の三角形三平方の定理 \(「a^2b^2=c^2」\) に \(a=3,b=5\) を代入すると \(3^25^2=c^2\) ⇔ \(925=c^2\) ⇔ \(34=c^2\) よって、\(c=\sqrt{34}\) となります。 \(\sqrt{34}\) は「\(34\) の正の平方 根」と言って、二乗したら \(34\) になる正の数のことを指します。 \(\sqrt{34}×\sqrt{34}=34\) Tooda Yuuto 具体的な値で表すと \(\sqrt{34}=51\cdots
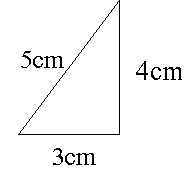
ですので、345とを使う場合は、角度を覚える必要はありません。 補足:例えば ABCで、AB=6cm,BC=8cm,∠B=90度ならば、 ピタゴラスの定理で計算しなくても345という比から AC=10cmが出せるということです。 も同様です。 一連の記事はこちら 三角比1|三角比を考え方から理解する!有名角の三角比も! 三角比2|sinθ, cosθ, tanθの超重要な4つの関係式 三角比3|実は当たり前!3つの(90°θ)型の変換公式 三角比4|角度が90°以上の三角比はこう考える! 三角比5|(180°θ)型の変換公式はめっちゃ簡単!が成り立ちます.(これを三平方の定理 根号の中を1つの数字に直してからルート(平方根のうちの正の方)を考えること は × は は × は 根号の中で2乗になっている数は外に出ると1つになる.1つしかないものは出られない. 根号の中に3個あるものは2個と1個に分ける 《問題2》 次の
3平方の定理 角度 1辺のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  | |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  |  |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 | 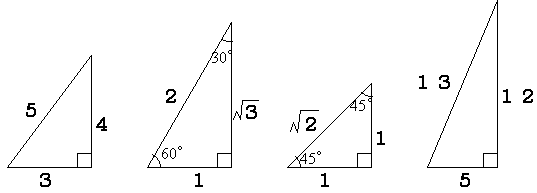 |  |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 |  | |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  | |
「3平方の定理 角度 1辺」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
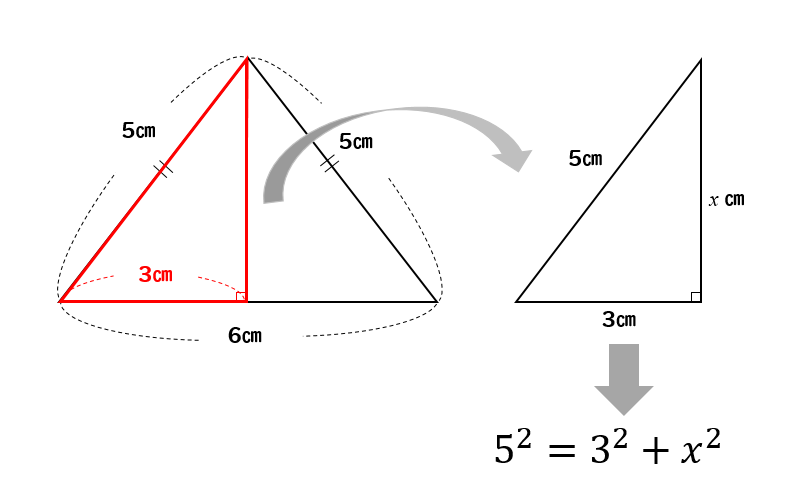 |  |
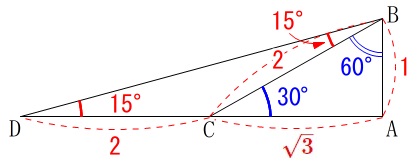
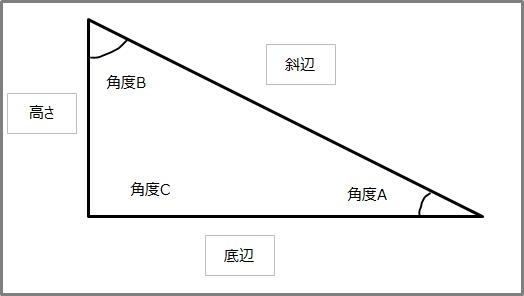
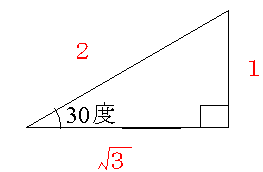
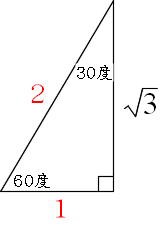
三平方の定理(ピタゴラスの定理)の応用問題パターン10選 三平方の定理(ピタゴラスの定理)は、直角三角形において成り立つ定理です。 また、どんな定理だったかと言うと、$3$ 辺の長さについての定理でした。もちろん暗記していなくとも三平方の定理で導けるのですが・・・ 非常によく使うので暗記すべきです。 辺の比と角度、両方暗記しておきましょう。 30° 60° 90° 次に、「正三角形半分タイプ」です。 \(3\) 辺の比が、\(12\sqrt{3}\) となることも暗記です。
Incoming Term: 3平方の定理 角度, 3平方の定理 角度 1辺,
コメント
コメントを投稿